Fracciones equivalentes, suma y resta de fracciones

Las fracciones pueden parecer un tema difícil al principio, pero en realidad son una forma muy útil de expresar cantidades que no son exactas o completas. Imagina que partes una pizza en ocho pedazos: si te comes tres, no comiste una pizza entera, pero comiste 3/8 de ella.

Ese tipo de representación es lo que llamamos una fracción. Hoy vamos a aprender sobre tres cosas importantes, qué son las fracciones equivalentes, cómo se suman fracciones y cómo se restan, todo con ejemplos muy claros para que niños de sexto de primaria puedan entenderlo sin complicaciones.

¿Alguna vez has partido una pizza? Imagina que tienes una pizza entera y la cortas en partes iguales. Cada pedazo representa una fracción. ¡Así de simples son las fracciones! Pero para dominarlas, en sexto de primaria necesitamos ir un paso más allá: aprender sobre fracciones equivalentes y cómo sumarlas y restarlas correctamente.

¿Qué es una fracción?

Antes de entrar en los temas más avanzados, recordemos: una fracción representa una parte de un todo. Si divides una barra de chocolate en 4 partes iguales y tomas una, estás tomando 1/4. El número de arriba (1) se llama numerador y el de abajo (4) se llama denominador.

Fracciones equivalentes

Ahora imagina que tomas esa misma barra de chocolate pero esta vez la divides en 8 partes. Si tomas 2 de esas partes, estás tomando 2/8. ¿Qué crees? Eso es lo mismo que 1/4. ¡Exacto! Son fracciones equivalentes.

Dos fracciones son equivalentes cuando representan la misma cantidad, aunque parezcan diferentes. ¿Cómo podemos comprobar que son equivalentes? Muy fácil: multiplicamos o dividimos el numerador y el denominador por el mismo número.

Ejemplo:
1/2 es lo mismo que 2/4, 3/6 o 4/8.

¿Por qué? Porque:

1 × 2 = 2 y 2 × 2 = 4 → 1/2 = 2/4

1 × 3 = 3 y 2 × 3 = 6 → 1/2 = 3/6

Y así sucesivamente. Solo necesitas usar el mismo número para multiplicar el numerador y el denominador.

Fracciones equivalentes: ¿por qué son tan importantes?

Cuando hablamos de fracciones, a veces dos fracciones que se ven distintas representan lo mismo. Por ejemplo, si tienes 1/2 de una pizza y tu amigo tiene 2/4, ¡ambos tienen la misma cantidad de pizza! A estas fracciones que parecen diferentes pero son iguales les llamamos fracciones equivalentes.

¿Cómo puedes comprobar si dos fracciones son equivalentes? Puedes multiplicar o dividir el numerador (el número de arriba) y el denominador (el de abajo) por el mismo número. Si obtienes otra fracción válida, entonces son equivalentes. Por ejemplo:

1/2 = 2/4 (porque 1×2 = 2 y 2×2 = 4)

Esto es muy útil cuando necesitamos sumar o restar fracciones, porque a veces las fracciones no tienen el mismo denominador y necesitamos convertirlas a equivalentes con denominadores iguales para poder operarlas.

Suma de fracciones paso a paso

Supongamos que tienes 1/4 de una barra de chocolate y luego te comes 2/4 más. ¿Cuánto comiste en total?

1/4 + 2/4 = 3/4

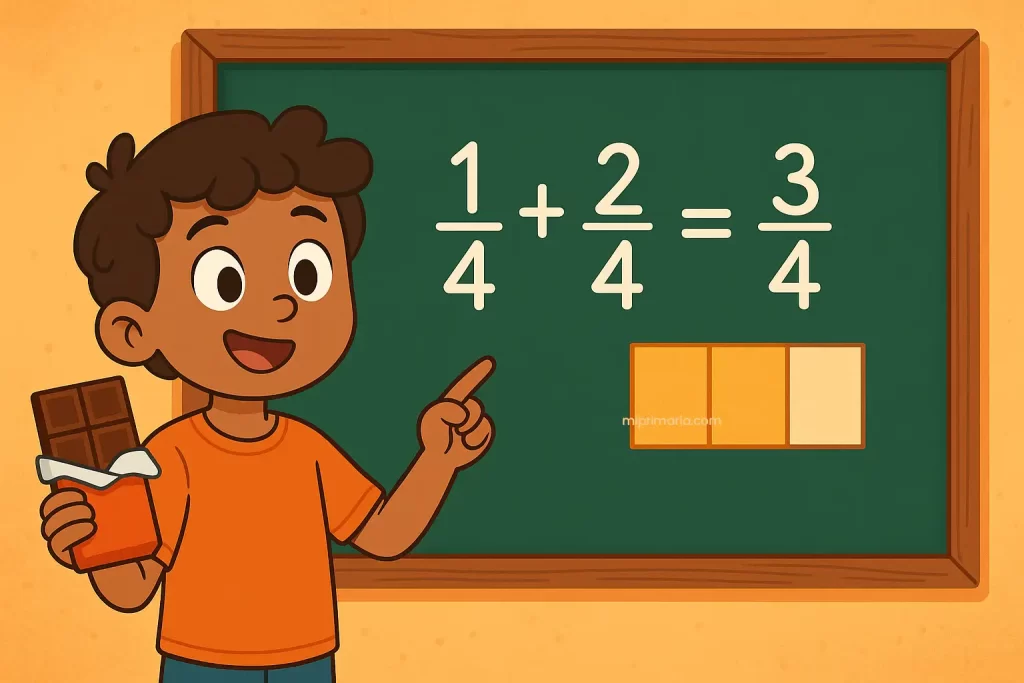
Como los denominadores ya son iguales, puedes simplemente sumar los numeradores. Fácil, ¿no?

Pero, ¿qué pasa si los denominadores son diferentes?

Vamos a ver este ejemplo: 1/3 + 1/6

Aquí no podemos sumar directamente porque los denominadores no son iguales. Entonces buscamos un número que sea múltiplo de ambos (el mínimo común múltiplo o mcm). En este caso, el mcm de 3 y 6 es 6.

Entonces convertimos 1/3 a una fracción con denominador 6:
1/3 = 2/6

Ahora sí podemos sumar:
2/6 + 1/6 = 3/6

Y si reducimos la fracción, 3/6 = 1/2

Así que, en total, tendríamos media unidad.

Resta de fracciones para niños

Imagina que tienes 5/8 de una pizza y tu hermano se come 2/8. ¿Cuánto te queda?

5/8 – 2/8 = 3/8

Como los denominadores son iguales, restamos los numeradores. Sencillo.

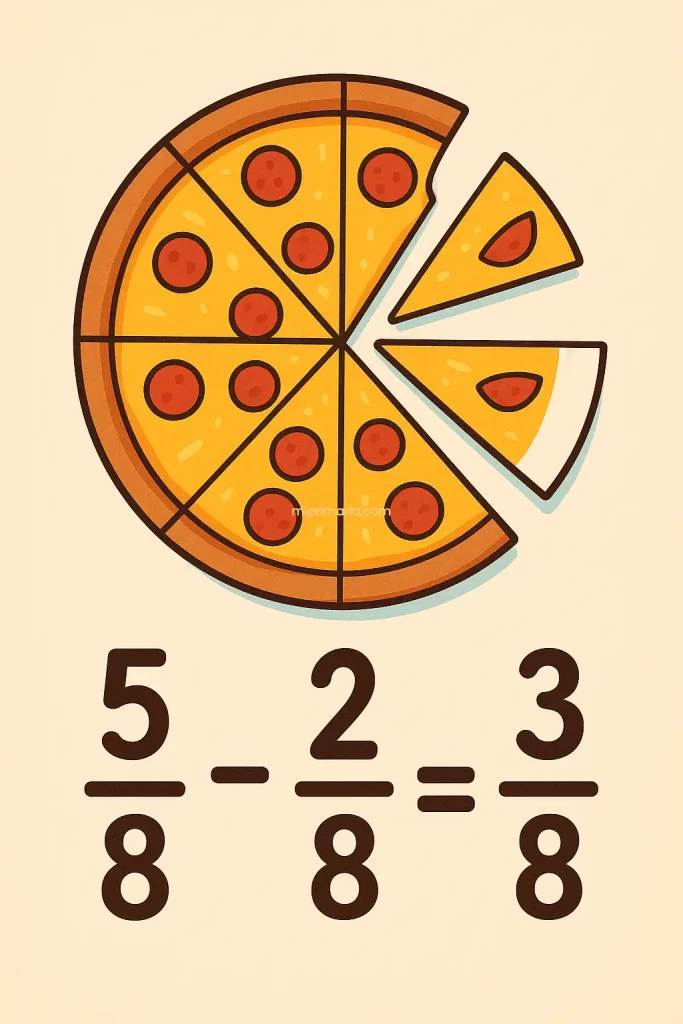
Ahora, ¿y si fueran fracciones con distintos denominadores? Como 3/4 – 1/6

Buscamos el mínimo común denominador (mcm de 4 y 6 es 12).

Convertimos ambas fracciones:
3/4 = 9/12
1/6 = 2/12

Entonces:
9/12 – 2/12 = 7/12

Listo. Esa es la cantidad que queda.

Tal vez pienses que las fracciones no se usan mucho fuera de la escuela, pero eso no es cierto. Se usan en recetas de cocina, al repartir comida o dulces, al dividir materiales en talleres, al leer relojes con minutos y segundos, ¡y mucho más!

Por ejemplo, si una receta dice 3/4 de taza de harina y solo tienes una taza medidora de 1/4, necesitarás usarla tres veces. O si estás jugando con tus amigos y quieren dividir una pizza en partes justas, las fracciones serán tus aliadas.

Practiquemos ¿puedes resolver este reto?

Tienes 2/3 de una botella de agua y bebes 1/6. ¿Cuánto te queda?

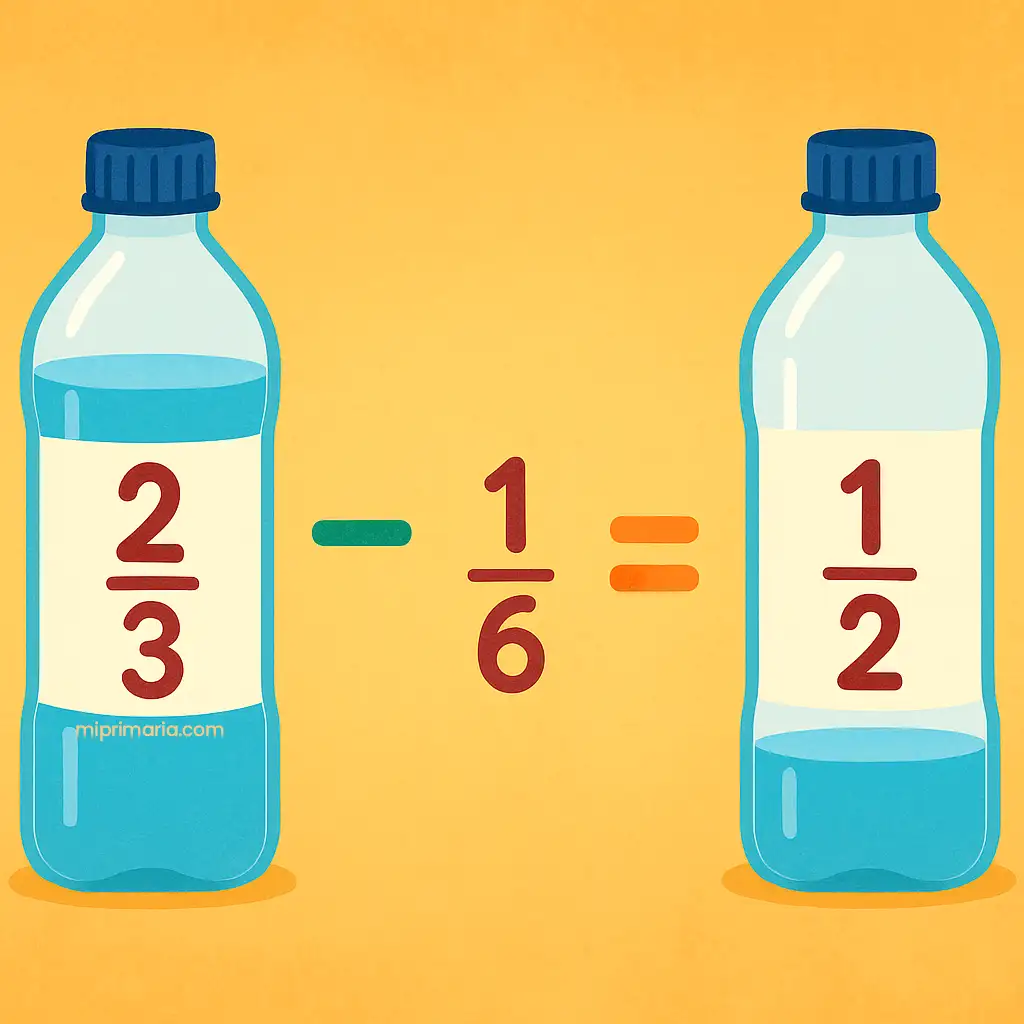
Primero, encontramos el mínimo común denominador de 3 y 6, que es 6.

2/3 = 4/6
Entonces:
4/6 – 1/6 = 3/6 = 1/2

Te queda media botella.

Y si lo piensas, eso tiene sentido. Bebiste una parte pequeña y quedaste con la mitad.

Las fracciones equivalentes, la suma y la resta de fracciones son herramientas matemáticas que usamos todo el tiempo sin darnos cuenta. Aprenderlas no solo te ayudará en exámenes o tareas, también te dará poder para entender mejor el mundo que te rodea. Recuerda: no se trata de memorizar reglas, sino de comprender lo que pasa en cada paso. Y cuanto más practiques, más fácil se vuelve.

Ahora que ya entendiste qué son las fracciones equivalentes, vamos a adentrarnos más en su utilidad y cómo podemos usarlas para sumar o restar fracciones.

Ejemplos de fracciones equivalentes

Imagina que tienes dos rebanadas de pizza. Una tiene 1/2 y la otra tiene 2/4. Si las miras bien, verás que ambas representan la misma cantidad. ¡Sí! Porque 2/4 es equivalente a 1/2. A esto se le llama una fracción equivalente.

¿Por qué necesitamos saber esto? Porque cuando queremos sumar o restar fracciones que no tienen el mismo denominador, debemos buscar una fracción equivalente que sí tenga el mismo número abajo (el denominador).

Veamos un ejemplo real:

Supón que tienes 1/3 de una barra de chocolate y tu amigo tiene 1/6. ¿Cuánto chocolate tienen entre los dos? No puedes simplemente sumar 1 + 1 y 3 + 6, porque los pedazos no son iguales. Lo que tienes que hacer es encontrar un denominador común.

En este caso, el número 6 es un múltiplo común de 3 y 6. Entonces convertimos 1/3 en una fracción equivalente con denominador 6. Para hacerlo multiplicamos el numerador y denominador por 2: 1/3 = 2/6.

Ahora sí: 2/6 + 1/6 = 3/6

Y si simplificas 3/6, te queda 1/2. Así que juntos tienen media barra de chocolate.

¿Ves qué útil es encontrar fracciones equivalentes?

Ahora vamos con la resta. Supón que comiste 3/4 de una pizza y te quedaron 1/4. ¿Cuánto comiste? Puedes pensar: 3/4 – 1/4 = 2/4, lo cual es correcto, y si simplificas, te queda 1/2.

¡Atención! Esto es fácil cuando los denominadores son iguales. El problema surge cuando son distintos.

Imagina ahora que tienes 2/5 y quieres restar 1/3. No puedes hacerlo así como están porque 5 y 3 no son iguales. Necesitas buscar un número que sea múltiplo de ambos: en este caso, 15.

Convertimos:
2/5 = 6/15 (porque 2×3 y 5×3)
1/3 = 5/15 (porque 1×5 y 3×5)

Y ahora sí: 6/15 – 5/15 = 1/15

Ahora hablemos del mundo real.

Imagina que estás repartiendo dulces con tus amigos. Si tienes una bolsa con 3/4 de caramelos de un sabor y otra con 2/4 de otro, y los mezclas, estás sumando fracciones. Pero si quieres quitar 1/4 de los que no te gustan, estás restando fracciones. ¡Y eso pasa seguido!

Otro ejemplo: Estás en clase de arte y quieres pintar 2/3 de tu hoja de un color, pero ya pintaste 1/6. ¿Cuánto te falta? Aquí debes restar: 2/3 – 1/6.

Convertimos:
2/3 = 4/6 (2×2 / 3×2)
1/6 = 1/6

4/6 – 1/6 = 3/6 → que se simplifica a 1/2

Te falta la mitad de la hoja por pintar.

Recuerda, cuando sumas o restas fracciones, ¡nunca sumes los denominadores! Solo trabajas con los numeradores si ya tienes el mismo denominador.

Otro dato importante: practicar con fracciones te hace más ágil para resolver problemas de la vida real como recetas, mediciones, juegos de mesa, horarios y más.

Practica también reconociendo cuándo puedes simplificar una fracción. Si tienes 4/8, piensa: ¿puedo dividir ambos números entre un mismo número? Sí, entre 4: 4÷4 = 1 y 8÷4 = 2. Entonces 4/8 = 1/2.

Para entender mejor, toma un papel, dibuja un rectángulo, divídelo en 4 partes iguales y sombrea 2. Eso es 2/4. Ahora, divídelo en 2 partes iguales y sombrea 1. Eso es 1/2. Verás que ocupan el mismo espacio.

Fracciones equivalentes como 3/6 = 1/2, 4/8 = 1/2, o 6/12 = 1/2 se ven diferentes, ¡pero representan la misma cantidad!