Suma y resta de fracciones con diferente denominador

Seguramente ya has aprendido a sumar fracciones cuando los números de abajo (los denominadores) son iguales. Eso es fácil, ¿verdad? Pero, ¿qué pasa cuando los denominadores son distintos? ¿Ya no se pueden sumar?

En este artículo te voy a enseñar paso a paso cómo sumar y restar fracciones con diferente denominador de una forma muy sencilla. No necesitas ser un genio en matemáticas, solo tener paciencia, entender bien los ejemplos y practicar un poco.

Aquí no vamos a usar palabras difíciles ni explicaciones raras. Todo será claro, con ejemplos reales, como si estuviéramos platicando en clase. Porque aprender fracciones puede ser mucho más fácil de lo que imaginas, y hasta divertido cuando ves que realmente lo entiendes.

¿Qué es una fracción?

Antes de entrar de lleno en fracciones con diferente denominador, repasemos algo importante: ¿qué es una fracción?

Una fracción es una manera de representar partes de un todo. Por ejemplo, si cortas una pizza en 4 pedazos y te comes 1, eso se escribe como 1/4. El número de arriba (el 1) se llama numerador y muestra cuántas partes tienes. El número de abajo (el 4) se llama denominador y dice en cuántas partes se dividió la pizza.

¿Qué pasa cuando las fracciones tienen diferentes denominadores?

Imagina que tú tienes 1/4 de pizza y tu amigo tiene 1/3. ¿Quién comió más? ¿Cuánto comieron entre los dos?

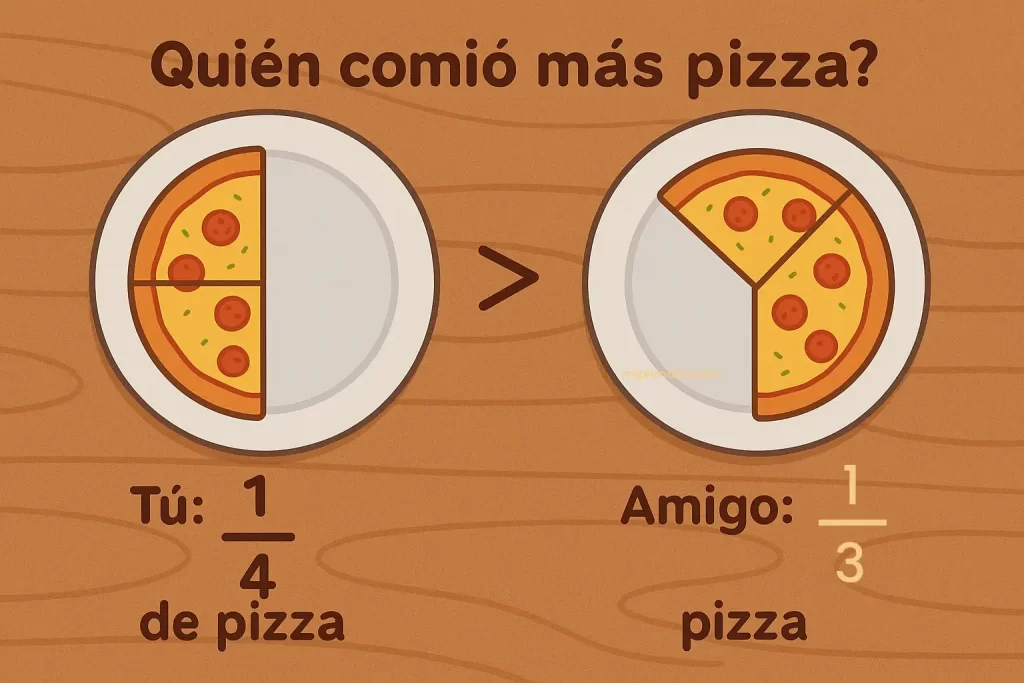
Aquí viene el problema: no puedes sumarlas directamente porque los pedazos no son del mismo tamaño. Un cuarto no es igual a un tercio.

Entonces, para poder comparar o sumar esas fracciones, necesitamos que tengan el mismo denominador. Es como si necesitáramos que todas las rebanadas fueran del mismo tamaño para poder contarlas correctamente.

¿Cómo se igualan los denominadores?

La clave está en encontrar un número que sea múltiplo de ambos denominadores. A ese número se le llama mínimo común denominador (MCD).

Por ejemplo, para 1/4 y 1/3, buscamos un número que esté en la tabla del 4 y también en la del 3. ¿Cuál es el primer número en común?

• Tabla del 4: 4, 8, 12, 16, 20…
• Tabla del 3: 3, 6, 9, 12, 15…

El 12 es el primero que se repite. Ese será nuestro nuevo denominador común.

Ejemplo: sumar 1/4 + 1/3 paso a paso

Ahora vamos a ver cómo sumar 1/4 + 1/3, pero con calma.

Paso 1: Busca el mínimo común denominador

Ya lo hicimos: es 12.

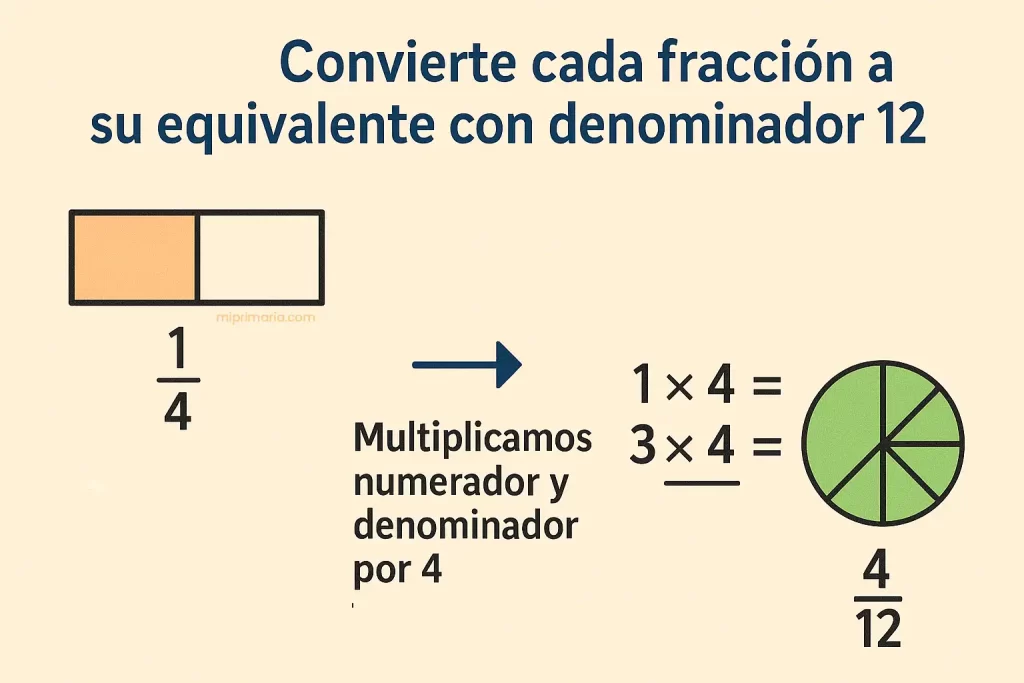
Paso 2: Convierte cada fracción a su equivalente con denominador 12

• Para convertir 1/4 en doceavos, pensamos: ¿por cuánto multiplicamos 4 para que dé 12? Por 3.
  Entonces multiplicamos también el numerador por 3:
  1 × 3 = 3, así que 1/4 = 3/12
• Para 1/3, multiplicamos el 3 por 4 para llegar a 12.
  Entonces 1 × 4 = 4, así que 1/3 = 4/12

Paso 3: Ahora que tienen el mismo denominador, las podemos sumar

3/12 + 4/12 = 7/12

¡Listo! Juntos comieron 7/12 de pizza.

¿Y si hay que restar?

No te preocupes, el proceso es igual. Lo único que cambia es que en lugar de sumar los numeradores, los restas.

Ejemplo: 5/6 – 1/4

Paso 1: Encuentra el mínimo común denominador

• Tabla del 6: 6, 12, 18, 24…
• Tabla del 4: 4, 8, 12, 16, 20…

El 12 es el número en común más pequeño. Ese será nuestro denominador.

Paso 2: Convierte las fracciones

• 5/6 en doceavos: 6 × 2 = 12 → 5 × 2 = 10 → 5/6 = 10/12
• 1/4 en doceavos: 4 × 3 = 12 → 1 × 3 = 3 → 1/4 = 3/12

Paso 3: Resta

10/12 – 3/12 = 7/12

¡Y así de sencillo!

Aprender a sumar o restar fracciones con diferente denominador no es solo algo para la escuela. Nos sirve para:

1. Cocinar, cuando usamos diferentes medidas
2. Repartir cosas entre amigos o familia
3. Entender descuentos o porcentajes
4. Resolver problemas de matemáticas en secundaria o más adelante

Trucos para facilitar el proceso

Aquí te comparto algunos consejos que pueden ayudarte sin hacer la explicación muy matemática:

1. Si los números de abajo (denominadores) son muy diferentes, no te estreses. Empieza sacando sus múltiplos y busca el primero en común.
2. Si uno de los denominadores es múltiplo del otro, ese ya puede ser tu denominador común. Por ejemplo: 1/5 + 2/10 → 10 es múltiplo de 5, así que puedes usar 10 directamente.
3. Escribe tus fracciones grandes y claras, con espacio entre cada paso. No trates de hacerlo todo en la cabeza.

Imagina esto:

En una fiesta hay dos pasteles iguales. Uno se parte en 6 pedazos y otro en 8. Tú te comes 2/6 del primer pastel y luego 3/8 del segundo.

La pregunta es: ¿Cuánto comiste en total?

Paso 1: Encuentra el mínimo común denominador

• 6 y 8 tienen como común múltiplo el 24.

Paso 2: Convierte las fracciones

• 2/6 → ¿6 × qué da 24? → ×4 → 2 × 4 = 8 → 2/6 = 8/24
• 3/8 → 8 × 3 = 24 → 3 × 3 = 9 → 3/8 = 9/24

Paso 3: Suma

8/24 + 9/24 = 17/24

Comiste 17/24 de pastel. ¡Casi todo!

¿Siempre hay que simplificar la fracción?

Cuando terminas de sumar o restar, es buena idea revisar si se puede simplificar. Eso significa hacerla más pequeña sin cambiar su valor.

Por ejemplo, si terminas con 6/12, puedes dividir arriba y abajo entre 6:

6 ÷ 6 = 1
12 ÷ 6 = 2

Entonces, 6/12 = 1/2

Esto ayuda a ver los resultados más claros y bonitos. Aunque en la escuela a veces no es obligatorio simplificar, te dará puntos extra si lo haces.

¿Y si son más de dos fracciones?

También se puede. Solo necesitas seguir el mismo procedimiento.

Por ejemplo:

1/2 + 1/3 + 1/4

Paso 1: El mínimo común denominador para 2, 3 y 4 es 12.

Paso 2:

• 1/2 → ×6 → 6/12
• 1/3 → ×4 → 4/12
• 1/4 → ×3 → 3/12

Paso 3:
6/12 + 4/12 + 3/12 = 13/12

En este caso, como el numerador (13) es más grande que el denominador (12), tenemos una fracción impropia. Eso significa que el resultado es más de uno.

Puedes dejarlo así o convertirlo en número mixto:
13/12 = 1 entero y 1/12

Consejos para no confundirte

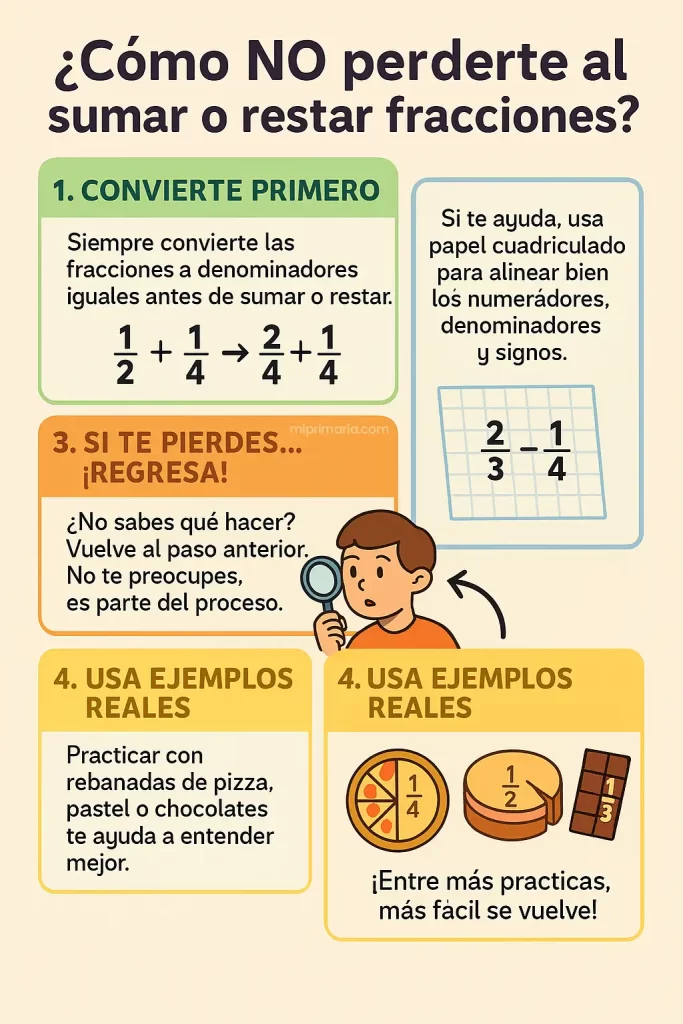
1. Siempre convierte las fracciones primero antes de sumar o restar.
2. Usa papel cuadriculado si te ayuda a mantener alineadas las fracciones.
3. Si te pierdes en un paso, regresa al anterior. No pasa nada.
4. Practicar con ejemplos reales (como rebanadas de pizza, pasteles o chocolates) hace que se te quede mejor.

Puede parecer complicado al inicio, pero como has visto, sumar o restar fracciones con diferente denominador es solo cuestión de paciencia y práctica. Lo más importante es encontrar un denominador común, convertir las fracciones y luego sumar o restar los numeradores.

Y recuerda no es solo para pasar el examen. Las fracciones están por todos lados en la vida real.

Sigue practicando, usa ejemplos de tu día a día y verás cómo poco a poco se vuelve natural.

¿Qué pasa si la fracción es mayor a un entero?

A veces, después de sumar dos fracciones con diferente denominador, te queda un resultado un poco raro ósea, el número de arriba (el numerador) es más grande que el de abajo (el denominador). ¿Qué significa eso?

Significa que tienes más de una unidad completa. A estas fracciones se les llama fracciones impropias. Pero no te asustes con el nombre, no tiene nada de malo. Solo es una forma diferente de escribir una cantidad que en realidad es más de uno.

Por ejemplo, si después de sumar terminas con 13/12, eso quiere decir que tienes 13 partes de algo que originalmente se divide en 12 partes iguales. Es como si tuvieras una unidad entera (los 12/12) y una parte extra (1/12).

Entonces, lo que hacemos es convertir esa fracción impropia en un número mixto. Un número mixto es simplemente un número entero junto a una fracción.

Vamos a explicarlo paso a paso:

Imagina que sumas dos fracciones y te queda 13/12.

Lo primero que piensas es: ¿cuántas veces cabe el número 12 en 13? La respuesta es 1 vez, porque 12 cabe una vez en 13, y sobra 1.

Ese 1 que cabe completo será tu número entero.
El sobrante (ese 1 que queda para llegar a 13) se convierte en el numerador de tu nueva fracción, y el denominador se queda igual: 12.

Entonces:
13/12 = 1 entero y 1/12
Así lo escribimos: 1 1/12

Ahora ya no solo tienes una fracción larga con un numerador más grande que el denominador. Tienes un número mixto que dice: “tengo 1 unidad completa y un pedacito más”.

Otro ejemplo para que lo entiendas mejor

Supón que terminas con 17/8.

Pregúntate: ¿cuántas veces cabe el 8 en el 17?
La respuesta es 2 veces (porque 8 x 2 = 16), y sobra 1 para llegar a 17.

Entonces:

• El número entero será 2
• La fracción será 1/8 (porque sobra 1)

Así que:
17/8 = 2 1/8

¿Por qué es útil convertir una fracción impropia en número mixto?

Porque te ayuda a visualizar mejor la cantidad que tienes. Decir que tienes 17/8 no dice mucho a simple vista, pero si dices que tienes 2 1/8, ya sabes que tienes dos unidades completas y un pedacito más. Esto se entiende mejor, sobre todo si estás hablando de cosas reales, como pasteles, litros de agua o metros de cuerda.

Además, en la mayoría de los exámenes y tareas, se valora que sepas hacer esta conversión. Es una forma de mostrar que entiendes bien lo que estás haciendo y no solo estás siguiendo pasos de memoria.